 |
|
 |
АНАЛИЗ ДЬЮРЕЙШН DURATION ANALYSIS АНАЛИЗ АКТИВОВ/ПАССИВОВ, к-рый включает измерение изменений стоимости реального основного капитала, возникающих в результате определенных изменений процентных ставок. Термин `дьюрейшн` был предложен в 1938 г. Маколеем (Macauley), к-рый задался вопросом: почему изменения процентных ставок вызывают изменения курсов облигаций, не являющиеся строго пропорциональными сроками их погашения? Он определил, что период, оставшийся до времени погашения облигации, является лишь частичным показателем продолжительности срока долгового обязательства, поскольку срок погашения не принимает во внимание объем промежуточных ден. потоков или их распределения во времени. Маколей разработал ряд формул для объяснения - чисто линейного - соотношения между курсами облигаций и изменениями процентных ставок. Ключевым показателем является `дьюрейшн` (мера процентного риска) облигации - средневзвешенный срок погашения, основанный на ТЕКУЩЕЙ СТОИМОСТИ ден. потоков (а не фактических потоков, как при обычном расчете среднего срока погашения). Данные понятия и лежат в основе анализа меры процентного риска
Расчет (измерение) дьюрейшн. Каждый вид активов подвержен нескольким видам рисков, в т. ч. кредитному риску, риску ликвидности, валютному риску, ценовому риску. Ден. потоки от каждого вида активов подвержены также реинвестиционному риску. Общий портфель банка подвержен и процентному риску.
`Дьюрейшн` представляет собой расчет меры процентного риска, основанный на ценовом и реинвестиционном рисках. Ценовой риск - это риск того, что процентные ставки возрастут, что вызовет уменьшение рыночной стоимости инвестиции; реинвестиционный риск - возможность падения процентных ставок, что ден. потоки от первоначальных обязательств могут быть реинвестированы по более низкой ставке, нежели их доходность. Очевидно, что ценовой и инвестиционный риски движутся в противоположных направлениях. Понижение курса облигации в связи с изменениями процентных ставок может быть напрямую привязано к мере процентного риска облигации.
Меру процентного риска облигации можно математически выразить следующим образом:
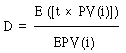
где t - период времени (в отличие от срока погашения), а PV(i) - текущая стоимость ден. потока в период t.
В качестве иллюстрации рассмотрим следующий пример:
Основная стоимость обязательства - 1000 дол.
Рыночная стоимость - 1000 дол.
Ставка купона - 10%
Доходность в момент погашения - 10%
Срок погашения - 5 лет
Процент, годовой - 100 дол.
Для составления уравнения потребуется сделать следующее:
1. Составить график ден. потоков по периодам.
2. Рассчитать текущую стоимость каждого ден. потока.
3. Умножить текущую стоимость ден. потока на номер его периода.
4. Разделить сумму полученных в п. 3. результатов на рыночную стоимость ценной бумагнных в п. 3. результатов на рыночную стоимость ценной бумаги.
Для простого примера расчет будет происходить следующим образом:
Период
1 2 3 4 5 Итого
Проценты 100 100 100 100 100 500
Основная сумма 0 0 0 0 1000 1000
Текущая стоимость 91 83 75 68 683 1000
Период ґ NPV 91 166 225 272 3415 4169
Т. о., `дьюрейшн`
4169
Дьюрейшн =--------- = 4,169
1000
В данном примере можно считать, что облигация с 5-летним сроком погашения дает 5 годовых ден. потоков плюс большой единовременный платеж. Первый ден. поток можно считать обязательством со сроком погашения один год с нулевой ставкой купона, а последний - обязательством с пятилетним сроком погашения с нулевой ставкой купона.
С точки зрения общей концепции, распространяя данный принцип на портфель, `дьюрейшн` в 4,169 означает, что по состоянию на 4,169 года, независимо от колебаний процентных ставок, доходность портфеля активов составила бы 10%, т. к. любое изменение реинвестиционного дохода за первые 4,169 года было бы нейтрализовано противоположным изменением рыночной стоимости в 4,169-й год, исходя из предположения, что пополнение портфеля и изъятия из него возможны и производятся. Для поддержания меры процентного риска портфеля на уровне 4,169 года и корректировки с учетом ее тенденции (тенденции мер процентного риска к изменениям во времени в результате изменений динамики ден. потоков) и изменений процентных ставок (напр., изменение процентных ставок с 10 до 11% изменяет меру процентного риска в приведенном примере в сторону повышения до 4,0) необходима способность к реструктуризации портфеля.
Каким будет изменение рыночной стоимости портфеля активов при конкретной величине `дьюрейшн`, если процентная ставка поднимется, допустим, на 100 процентных пунктов? Уравнение для расчета примерного изменения дано ниже:
- D(r) ґ текущий рыночный курс
Изменение рыночной стоимости = -----------------------------------------
(1 + r)
где D - мера процентного риска обязательства, r - текущая процентная ставка, и r - изменение процентной ставки.
Применительно к приведенному примеру:
-4,169(0,01) * 1000
Изменение рыночной стоимости =----------------------------- = -37,90
(1 + 0,10)
Иными словами, если ставки увеличиваются на 1%, то стоимость портфеля активов сокращается примерно на 37,90 дол. Точность данного расчета уменьшается по мере увеличения `дьюрейшн` и изменений ставок (точная цифра снижения рыночной стоимости в приведенном выше примере равна 36,96 дол.).
Если рассмотреть `дьюрейшн` с другой точки зрения, то она представляет собой срок погашения облигации с нулевым купоном, к-рая имеет ту же доходность на момент погашения, что и альтернативная купонная облигация, и будущую стоимость при величине `дьюрейшн` рассчитанных и учтенных ден. потоков купонной облигации на дату `дьюрейшн`. В приводимой ниже таблице показан расчет эквивалента облигации с нулевым купоном:
1 $100 $135,27
2 100 122,98
3 100 111,80
4 100 101,63
5 1100 1016,32
$1488,00
Изменение процентных ставок повлияет на текущую стоимость двух данных ценных бумаг сходным образом, пока их `дьюрейшн` остается одинаковой:
9 $1039
10 1000
11 963
Вместе с тем, независимо от изменений процентной ставки, облигация с нулевым купоном на момент ее приобретения дает доход при погашении не только на первоначальное вложение капитала, но и на реинвестированный процент. Она не подвержена ценовому или реинвестиционному рискам, если находится у держателя до наступления срока погашения.
Эквивалентная купонная облигация будет иметь те же характеристики; ее ценовой риск при продаже (в данном случае - 4,169 года) будет нейтрализовывать любой реинвестиционный риск, существующий до этого (если предположить, что динамика процентных ставок при их изменении является параллельной). Однако при получении кассовых платежей по купонной облигации ее `дьюрейшн` может изменяться по сравнению с первоначальной эквивалентной облигацией с нулевой ставкой, что потребует корректировки портфеля для сохранения нулевого купона.
Балансирование активов и пассивов. Упрощенным подходом к управлению активами и пассивами является балансирование фонда и актива с обязательством равного срока погашения при положительной разнице и игнорирование периодических ден. потоков, поступающих от актива, а также его `дьюрейшн`. Чем выше текущий доход по ценной бумаге, тем больше ее ден. поток и короче `дьюрейшн` или период возмещения затрат. Эти ден. потоки будут оказывать влияние на доход при их реинвестировании по ставкам выше или ниже ставок по первичному обязательству и, т. о., повлияют также на фактическую доходность по первичному обязательству при его погашении.
При данном анализе `дьюрейшн` балансируют портфели активов/пассивов, а не сроки погашения активов и пассивов. Напр., при наличии портфеля, в к-ром рыночная стоимость активов равна 100, рыночная стоимость пассивов равна 95, а рыночная стоимость акционерного капитала (остаточная величина) равна 5, `дьюрейшн` активов и пассивов рассчитывается, соответственно, как 5 лет и 4 года. Предположим, что процентные ставки возрастают на 200 базисных пунктов. Используя уравнение для изменения рыночной стоимости, получаем новую стоимость:
Изменение рыночной стоимости + Первоначальная стоимость =
= Новая стоимость стоимости
-5(2,0) *100
Для активов:---------------- = -$9,09 $100 $91
(1 + 0,10)
-4(2,0) ґ 95
Для пассивов:-------------- = -$6,90 $95 $88
(1 + 0,10)
Стоимость акционерного капитала $3
В данном случае, поскольку стоимость активов упала на большую сумму, чем коэффициент обязательств, стоимость акционерного капитала сократилась с 5 до 3. Покрытие капитала, составлявшее 5%, снизилось до 3,3%.
Акционерный капитал можно было бы защитить от такого падения стоимости, если бы `дьюрейшн` актива и пассива были сбалансированы таким образом, что `дьюрейшн` капитала составила бы 0, - иными словами, т. о., чтобы стоимость акционерного капитала была защищена от любых изменений процентных ставок. Уравнение для этого выглядит следующим образом:
(Da * Va) = (D1 * V1),
где D представляет собой `дьюрейшн`, а V - рыночную стоимость. Величина, представляющая стоимость акционерного капитала, из уравнения выпадает, поскольку его `дьюрейшн` установлена на нуле.
В стабильном банке стоимость активов (Va) должна превышать стоимость пассивов (V1). Т. о., для их балансирования `дьюрейшн` активов (Da) должна быть меньше, чем `дьюрейшн` пассивов (D1). Предположим, что `дьюрейшн` и стоимость портфеля активов равны соответственно 5 и 100, а стоимость портфеля пассивов равна 95, как и в приведенном примере; тогда желаемая величина `дьюрейшн` пассивов составляет:
5 * 100 = D1* 95
5,26 = D1
Снова предположим, что процентные ставки выросли на 200 базисных пунктов. Новые величины будут следующими:
Изменение рыночной стоимости + Первоначальная стоимость =
= Новая стоимость стоимости
-5(2,0) * 100
------------------= $9,10 $100 $91
(1 + 0,10)
-5,26(2,0) * 95
---------------------= $9,08 $95 $86
(1 + 0,10)
Стоимость акционерного капитала $5
Номинальный основной капитал был защищен от изменений ставки, а покрытие капитала увеличилось до 5,49%. Если бы `дьюрейшн` активов и пассивов были сбалансированы, то стоимость акционерного капитала снизилась бы, однако отношение акционерного капитала к покрытию капитала осталось бы равным 5%. Однако `дьюрейшн` портфелей активов и пассивов изменяются в ответ на любое изменение процентных ставок, поэтому банк должен осуществлять соответствующую реструктуризацию своих портфелей для нейтрализации изменений `дьюрейшн`.
Сдвиг дьюрейшн. Даже если процентные ставки не изменялись, а `дьюрейшн` портфелей активов и пассивов были изначально равными, то `дьюрейшн` активов и пассивов с течением времени изменяются в силу различия промежуточных ден. потоков (их распределения во времени и величины), полученных от активов и пассивов. Это изменение называется сдвигом `дьюрейшн`.
Сдвиг `дьюрейшн` вызван также различными темпами возмещения затрат по активам с промежуточными ден. потоками и единичным ден. потоком облигаций с нулевым купоном. `Дьюрейшн` актива с промежуточными ден. потоками будет снижаться нелинейным образом, поскольку текущая стоимость дохода, полученного в первые годы, выше текущей стоимости дохода, полученного в более поздние годы. `Дьюрейшн` облигации с нулевым купоном снижается линейно из-за ее особенности - единственного платежа по ней. Несмотря на то, что портфель активов может состоять только из облигаций с нулевым купоном, с портфелем пассивов такого не произойдет; поэтому `дьюрейшн` портфелей активов и пассивов будут по-разному реагировать на изменение процентной ставки и будут иметь тенденцию к расхождению.
Для поддержания сбалансированности `дьюрейшн` своих портфелей таким образом, чтобы `дьюрейшн` акционерного капитала равнялась 0, банк должен держать структуру своих активов и пассивов под постоянным наблюдением, производя соответствующие изменения в сроках погашения или ставках по купонам по активам, пассивам либо тем и другим (изменения должны происходить в противоположном направлении).
Развитие анализа дьюрейшн. Описанная выше модель принадлежит к первому поколению моделей анализа `дьюрейшн`, обычно называемых `дьюрейшн Маколея`. В основе этой модели лежит предположение о том, что кривые текущей процентной доходности реагируют на случайные события параллельными сдвигами кривых доходности. Однако такое нереалистическое предположение могло бы привести к нереалистическим результатам. Можно создать портфель очень краткосрочных и очень долгосрочных инвестиций с такой же `дьюрейшн`, как и у портфеля среднесрочных инвестиций. Если изменения на концах кривой доходности отличаются от изменений в ее средней части, то состояние двух портфелей может быть весьма различным, как на собственном горьком опыте убедились многие служащие банка, занятые инвестиционными операциями.
Анализ `дьюрейшн`, принадлежащий ко второму поколению, включает дисконт кривой доходности или учет значимых курсов `спот` (курсов по наличным сделкам) по облигациям с нулевыми купонами на каждый год до срока погашения. Затем каждый ден. поток дисконтируется на величину значимого курса за год, в течение к-рого поступает ден. поток. Анализ `дьюрейшн`, принадлежащий к третьему поколению, включает корректировку кривой доходности со значимым курсом `спот` по облигациям с нулевыми купонами для определения средней неустойчивости курсов за прошлые периоды и для использования этих данных для прогноза. Для анализа четвертого поколения требуется эмпирическое изучение случайных событий, влияющих на определение краткосрочных и долгосрочных курсов, и создание на основе этого анализа прогнозов относительно неустойчивости курсов.
Общий недостаток всех этих моделей состоит в том, что, хотя основной расчет `дьюрейшн` является простым, получение верных значений для использования в данных расчетах весьма затруднительно. Банк прежде всего должен располагать адекватными данными о портфеле и использовать их для составления адекватного графика ден. потоков в течение времени инвестиций. Однако вследствие досрочного погашения или непогашения обязательств фактические ден. потоки могут отличаться от установленных договором. Поэтому для более точной оценки ден. потоков банк должен оценить вероятность досрочного погашения или непогашения ден. потоков.
Следующий шаг - дисконтирование ожидаемых ден. потоков, что требует некоторых предположений относительно динамики кривых доходности. Существует несколько моделей кривых доходности, к-рые являются более сложными, нежели простая кривая текущей доходности, однако ни одна из них, взятая по отдельности, не может обеспечить безошибочный расчет `дьюрейшн`.
Дополнительным осложнением является выбор правильных курсов, по к-рым нужно дисконтировать ден. потоки. События, воздействующие на процентные ставки, по-разному отразятся на краткосрочных и долгосрочных курсах. Это различие следует принимать во внимание при расчете влияния изменений курса на `дьюрейшн` любого данного портфеля.
Т. о., анализ `дьюрейшн` не дает окончательных цифр, а предоставляет лишь оценки, основанные на определенных предположениях. Это не панацея, но он может быть очень полезным инструментом для управления активами и пассивами. (Адаптировано из работы: Leonard E. Wyderko, Jr. Duration Analysis Primer, Bank Administration Institute, 1985).
См. АНАЛИЗ `ЗАТРАТЫ-ВЫПУСК`; АНАЛИЗ `ПРИБЫЛЬ-ЗАТРАТЫ`; АНАЛИЗ ПРОМЕЖУТКА ВРЕМЕНИ; ИММУНИЗАЦИЯ.
БИБЛИОГРАФИЯ:
BANK ADMINISTRATION INSTITUTE. A Duration Analysis Primer. Bank Administration Institute, Rolling Meadows, IL, 1985.
. A Practical Guide to Duration Analysis. Bank Administration Institute, Rolling Meadows, IL, 1988.
Начало
|
|

